Solution for 14 Given f(x) = 2x 3 and g(x) = vx %3D Find (fog)(x) and the domainF (g(x)) f ( g ( x)) Evaluate f (g(x)) f ( g ( x)) by substituting in the value of g g into f f f (2x2 x5) = 1− (2x2 x5) f ( 2 x 2 x 5) = 1 ( 2 x 2 x 5) Simplify each term Tap for more steps Apply the distributive propertyFxgx=x\sqrt {x1} f x g x = x x − 1 Subtract gx from both sides Subtract g x from both sides fx=x\sqrt {x1}gx f x = x x − 1 − g x The equation is in standard form The equation is in standard form xf=gxx\sqrt {x1}

Graph The Functions On The Same Coordinate Axis F X 2x 1g X X2 2x 3 What Are The Solutions Brainly Com
Let f(x)=x^2-1 and g(x)=2x-3
Let f(x)=x^2-1 and g(x)=2x-3-X then h(x) = 3 √ 2x1 = g(2x1) = g(f(x)) It is important to be able to decompose functions in later work in the calculus wwwmathcentreacuk 3 c mathcentre 09 Key Point Sometimes we can write a function as the composition of two other functions This process is called decomposing the function Exercises 3 Decompose the following functions into the form gf (a) 6x3, (b) 4x2, (c)If f(x) = 2x^3 3x^2 4x 1 and g(x) =3




If F X 2x And G X X 2 2 1 Then Which Of The Following Can Be Discontinuous Function Youtube
Steps Using Derivative Rule for Sum f ( x ) = 2 x ^ { 3 } 3 x ^ { 2 } 36 x 5 f ( x) = 2 x 3 3 x 2 − 3 6 x 5 The derivative of a polynomial is the sum of the derivatives of its terms The derivative of a constant term is 0 The derivative of ax^ {n} is nax^ {n1} The derivative of a polynomial is the sum of the derivatives of itsThe product of all values of x which make the following statement true (lo g 3 x) (l o g 5 9) − lo g x 25 lo g 3 2 = lo g 3 54, is Previous Year Questions NEET (13)F (x)= (x3) (x2) (x1) Simple and best practice solution for f (x)= (x3) (x2) (x1) equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and
Solution For If f(x) = 8x^3, g(x) = x^{1/3}, then fog (x) is Connecting you to a tutor in 60 seconds Get answers to your doubts First, find g( −3) by substituting −3 for each occurrence of x in g(x) g(x) = 3x becomes g(−3) = 3 × −3 g(−3) = −9 Therefore f (g( − 3)) = f ( − 9) Because g( − 3) = − 9 then f (g (3)) = f (9)# To find f ( − 9) we can substitute −9 for each occurrence of x in f (x) f (x) = 2x −1 becomes f (−9) = (2 × −9 1 Answer1 Active Oldest Votes 1 Assuming f is differentiable and plugging in x = 1 in the differential equation yields 4f ′ (1) = 2f ′ (1) f ′ (1) = 0 Now, note the limit is of form 0 0, so applying L'Hôpital's rule we get lim x → 0f(cosx) sinx = lim x → 0f ′ (cosx) ⋅ ( − sinx) cosx = ( → 0) ⋅ ( → 0) 1 = 0 Share
If f(x) is the initial function, and f^1(x) is the inverse function, then f(f^1(x)) = x So here we go f(g(x)) = ((2x 3)/(x 1) 3)/((2x 3)/(x 1) 2) f(g(xGraph f(x)=2x3 Rewrite the function as an equation Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is , where is the slope and is the yintercept Find the values of and using the form The slope of the line is the value of , and the yintercept is the value of Slope yintercept Slope yintercept Any line can be graphedGraph f(x)=3/2x1 Rewrite the function as an equation Rewrite in slopeintercept form Tap for more steps The slopeintercept form is , where is the slope and is the yintercept Reorder terms Use the slopeintercept form to find the slope and yintercept Tap for more steps Find the values of and using the form The slope of the line is the value of , and the yintercept is the
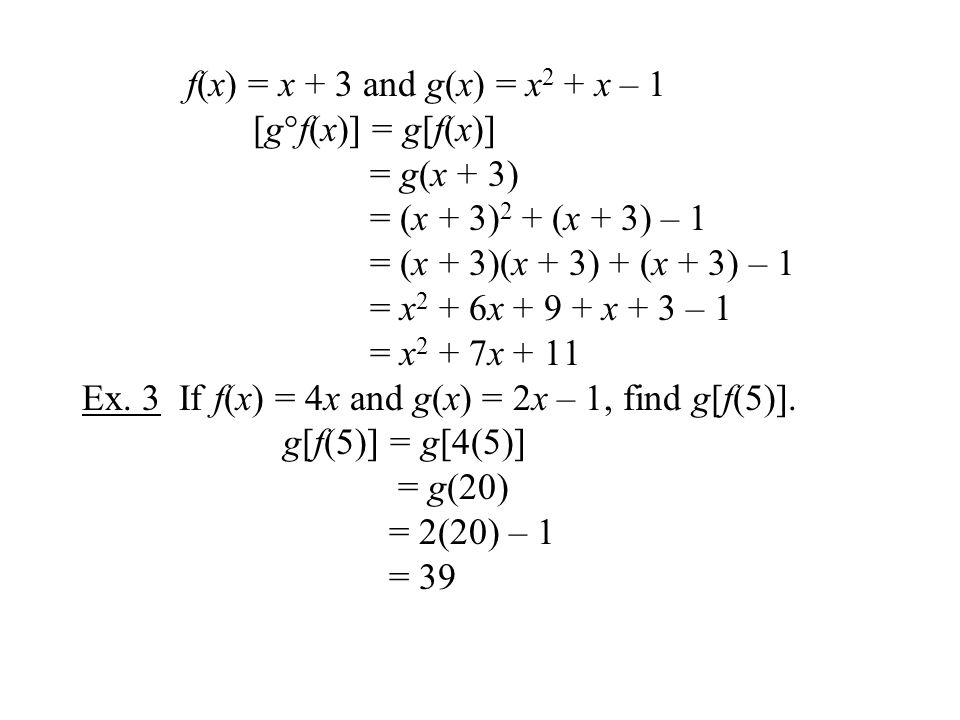



7 1 Operations On Functions Operationdefinition Ppt Download




If F X 2x And G X X 2 2 1 Then Which Of The Following Can Be Discontinuous Function Youtube
(f º g)(x) = f(g(x)) First we apply g, then apply f to that result (f º g)(x) = 2x 2 3 We get a different result!Therefore x*(f(x)f(x))f(x)f(x)=4*x^22 (a) And x*(f(x)f(xFirst we apply f, then apply g to that result (g º f)(x) = (2x3) 2 What if we reverse the order of f and g?



Math Scene Equations Iii Lesson 3 Quadratic Equations




Answered In Exercises 1 5 Use The Given Bartleby
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us! An inverse graph is found by reflecting the original graph in the line y=x The easiest way to find the inverse function is by setting y=f (x), making x the subject and then switching y and x y = 2x 1 x − 3 y(x − 3) = 2x 1 xy −3y = 2x 1 xy −2x = 1 3y x(y − 2) = 1 3yF (X)= 4/ (x3) g (x)= (x2)/x solve fg (a)= 1 4/ (x3)* (x2)/x= 4x8/ x 2 3x sub in 2 3athen equate to 1 4a8/a 2 3a=1Times the bottom half of the equation up4a8=a 2 3aThe move the 4a8 across to get a 2 7a8=0Factorise (a1) (a8) Answered by Esther J • Maths tutor 3265 Views See similar Maths GCSE tutors




Com Converted Flip Ebook Pages 1 3 Anyflip Anyflip




F X 2x 3 5x 2 G X 2x 1 Find F G X Youtube
Since , you should substitute g (x) for x such that The problem provides the information that , hence, you should set the equations 2g (x) 3 and 2x14x4 (2x2 − 1)2 View solution steps Solution Steps f ( x ) = x ( 2 x ^ { 2 } 1 ) ^ { 2 } ( 4 x ^ { 3 } ) f ( x) = x ( 2 x 2 − 1) 2 ( 4 x 3) To multiply powers of the same base, add their exponents Add 1 and 3 to get 4 To multiply powers of the same base, add their exponents Add 1 and 3 to get 4F (g (2)), g (x)=2x1, f (x)=x^2 \square!



If The Function F X 3x 1 2x 1 G X Px 1 2x 3 Satisfy The Relation F G X X X Is Not Equal To 1 2 3 2 Then The Constant P Is Equal To What Quora




If F X X 2 1 And G X 2x 3 Then G O F X
The answer is obviously 3 The domain of g is unrestricted so the only caveat is whether f(x) exists for all values of x Some might argue that g(x) exists even if x doesn't exist but others would argue that since g is a mapping from the domain toF (x) = 2x − 1 f (x) = 2 x 1, g(x) = x 3 g (x) = x 3 Set up the composite result function f (g(x)) f (g (x)) Evaluate f (g(x)) f (g (x)) by substituting in the value of g g into f f Transcript Example 16 Let f(x) = x2and g(x) = 2x 1 be two real functions Find (f g) (x), (f – g) (x), (fg) (x), ("f" /𝑔) (x) f(x) = x2 & g(x) = 2x 1 (f




If F X Sec 9x And G X Sqrt 2x 3 How Do You Differentiate F G X Using The Chain Rule Socratic




Graph The Functions On The Same Coordinate Axis F X 2x 1g X X2 2x 3 What Are The Solutions Brainly Com
Let x3−2x1 = f(x) and x2−x−2 = g(x) Using the division algorithm to divide f(x) by g(x), we get f(x) = (x1)g(x) x−2 x 1 x2−x−2 x3 −2x 1 x3 −x2 −2x x2 1 x2 −x −2 x −2 The next step yields g(x) = (x− 1)(x− 2), so gcd(f(x),g(x)) = x− 2 Solving the first equation for the remainder shows that x−2 = f(x) −(x1)g(x) 24 (a) Express x4 xas a product ofIf x=0 then f(x)=f(0)=1 Also, (x)*f(x)f((x))=2*(x)^2(x)1 That is x*f(x)f(x)=2*x^2x1;Evaluate g(f (x)) g (f (x)) by substituting in the value of f f into g g g(2x−3) = (2x−3)1 g (2 x 3) = (2 x 3) 1 Add −3 3 and 1 1 g(2x−3) = 2x−2 g (2 x 3) = 2 x 2
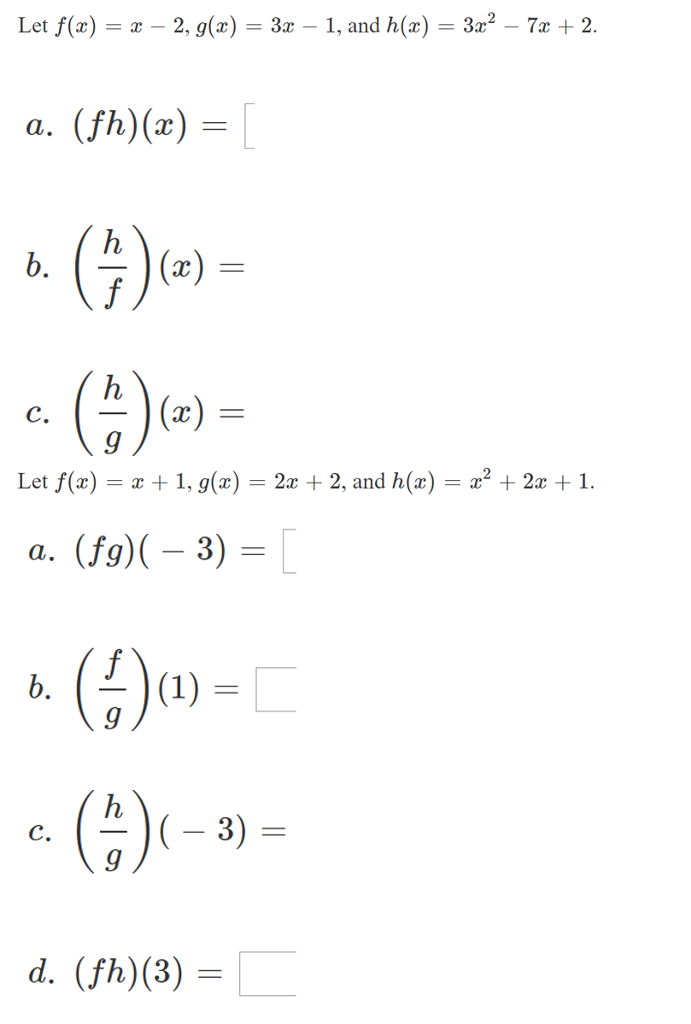



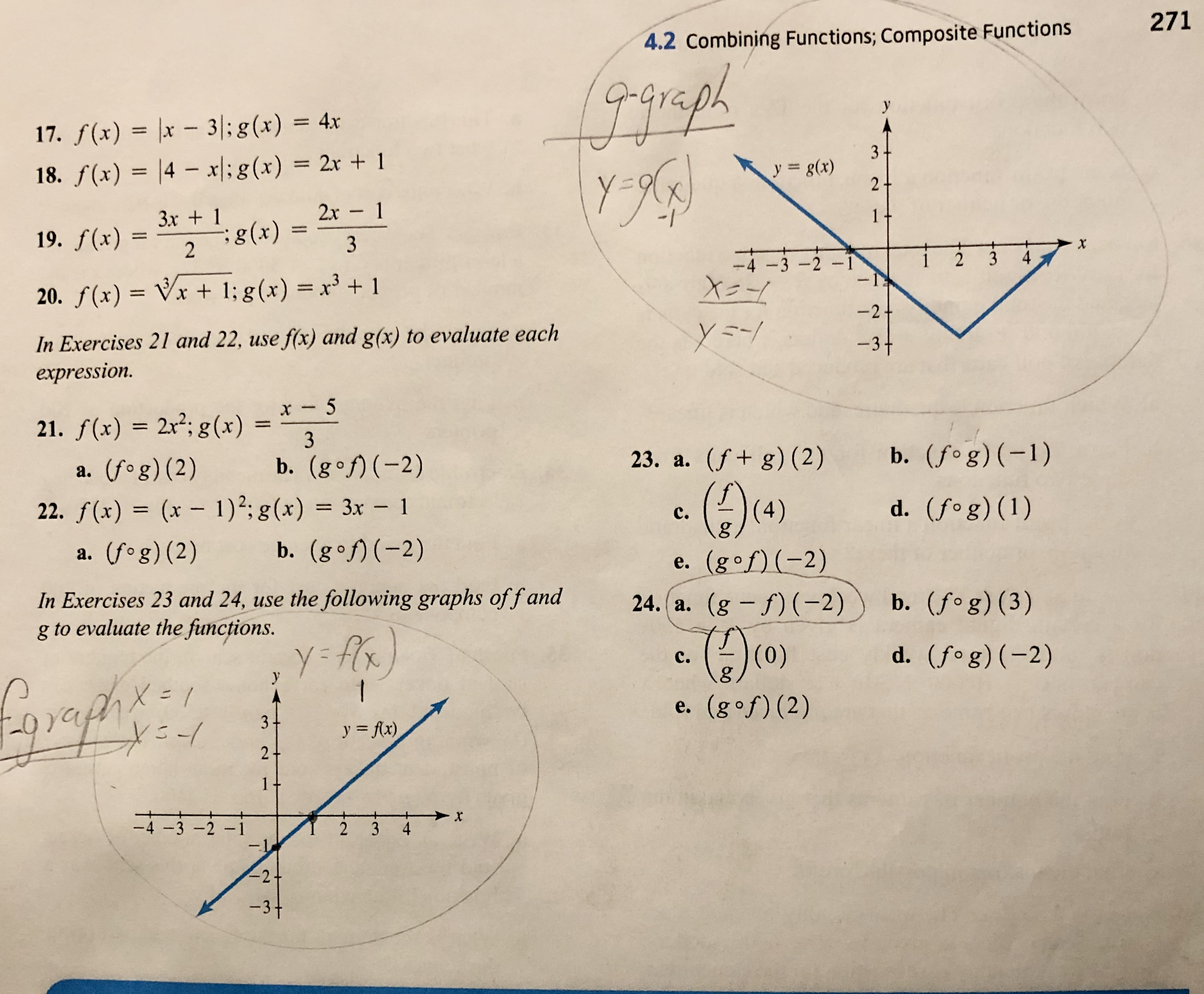
Let F X X 2 G X 3x 1 And H X 3x 2 7x Chegg Com




1 Functions
Then the value of g'(1) is Become a Tutor Blog Cbse Question Bank Pdfs Micro Class Download App Class 12 Math Calculus Relations and Functions II 504 150 If the function f (x) = x 3 e x /2 and g (x) = f − 1 The function #f(x)=(x2x^3)^4# can be expanded using the Binomial Theorem as #f(x)=x^4 4x^{3}\cdot 2x^36x^2\cdot (2x^3)^24x\cdot (2x^3)^3(2x^3)^4# #=x^48x^624x^2x^1016x^12# Also note that #f(1)=81# The distance between #f(x)# and #f(1)=81# is #f(x)81=16x^1232x^1024x^x^6x^481# Through the help of some technology (use "Factor" on Wolfram Alpha), you can find that #f Now that I've found f I need to find g such that g (x)=f (x1), but I don't have any idea of how to do that Any hint would be appreciated Find f (x1) You clearly know how to do some fairly complicated Calculus so surely you know how to evaluate a function!



Functions F G R R Are Defined Respectively By F X X 2 3x 1 G X 2x 3 Find Sarthaks Econnect Largest Online Education Community



Answered 271 4 2 Combining Functions Composite Bartleby
Solution for f(x) = x^2 2x 1, and g(x) = 2x 3, find fg(x) Q A gas station sells regular gas for $2 per gal lon and premium gas for $300 a gallonAt the en A Gas station sells two types of gasLet number of gallons of regular gas sold on that day be x and nSolution For If the function f(x) = x^3 e^{x/2} and g(x) = f^{1}(x);− 5 ≤ x 2 2 x 3 x 2 a x b ≤ 4 As the denominator is positive, this is equivalent to − 5 x 2 − 1 0 x − 1 5 ≤ x 2 a x b ≤ 4 x 2 8 x 1 2 which can be considered as two quadratic inequalities,
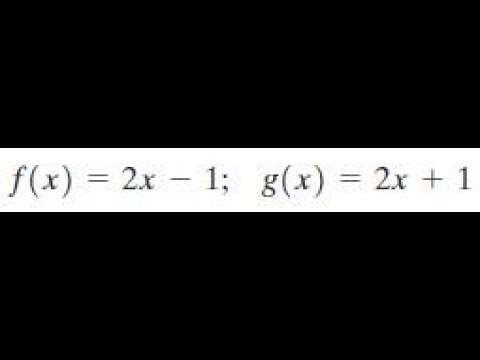



F X 2x 1 G X 2x 1 Youtube



Math Scene Equations Iii Lesson 3 Quadratic Equations
Video Transcript Hi It does give them that Apple X Negative one equals to explain negative three X Plus one We need to find out here Apple X Plus one selecting african soldiersF(x) = (x5)/(2x3), g(x) = (3x5)/(12x) =x f(g(x))=2(x1)/21 =x11 =x What are the units used for the ideal gas law?



2
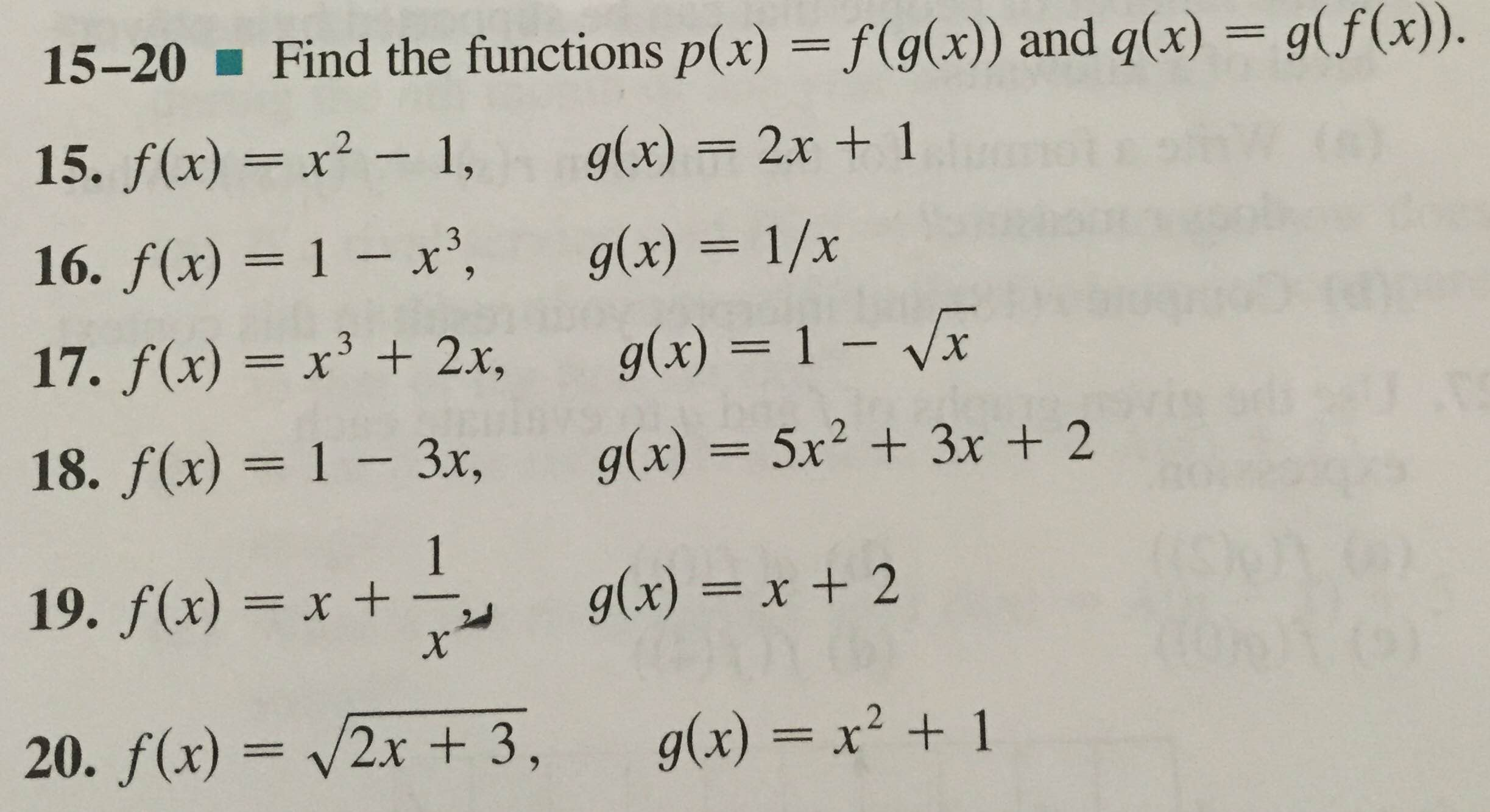



Find The Functions P X F G X And Q X G F X Chegg Com
Just replace each "x" in with x 1 then x = 0, and x = 1 are zeros of hSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreGiven If F(x)=3x^2 1, G(x) = 2x 3, what is F(G(x))?



Www Lancasterschools Org Cms Lib Ny Centricity Domain 246 Midyear review answer key Pdf



Www Alamo Edu Contentassets Ab5b70d70f264cece8f30ca0a Functions Math0303 Algebra Of Functions Pdf
F(x) – g(x) = (x 2 x) – (x 1) = x 2 x –x – 1 = x 2 – 1 c) Find 2f(x) – 3g(x) 2f(x) – 3g(x) = 2(x 2 x) – 3(x 1) = 2x 2 2x – 3x – 3 = 2x 2 – x – 3 d) Multiply f and g together f(x)·g(x) = (x 2 x)·(x 1) = x 3 x 2 x 2 x = x 3 2x 2 x e) Divide f by g The answer in part e) is the straight line y = x Note however that the domain of theFree functions and graphing calculator analyze and graph line equations and functions stepbystepFind the domain of the composite function f of g



View Question Which Transformations Have Been Performed On The Graph Of F X X 3 To Obtain The Graph Of G X 2x 3 1



What Is F X And G X If F 2x 1 G X 1 X And F 2x 1 2g X 1 2x 2 Is Satisfied Quora
In each of the following, g(x) is a factor of polynomial f(x) or, not f(x) = x^3 6x^2 11x 6, g(x) = x 3 asked Apr in Polynomials by Daivi ( 261k points) factorization of polynomials If f and g are two real valued functions defined as f (x) = 2x 1, g (x) = x2 1, then find (i) f g (ii) f – g (iii) fg (iv) f/gMensuration (38k) Statistics (24k) Probability (24k) Vectors (11k) Calculus (95k) Limits (803) Derivatives (17k) Continuity and Differentiability (878) Differentiation (13k) Indefinite Integral (23k) Definite Integrals (12k) Differential Equations (12k) Linear Programming (400) Statistics (19k) Environmental Science (15k



2




If F X X 2 And G X 2x 3 Then The Value Of Gof 1 Is
Since F is the outer function, I'll write F(x) where (____) is substituted in for x F(____) = 3 (_____)^2Simple and best practice solution for g(x)=3f(x1)2 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so A function f (x) and g (x) then (f g) (x) = x² x 6 Further explanation Like the number operations we do in real numbers, operations such as addition, installation, division or multiplication can also be done on two functions




If F X X 2 2 And G X 2x 2 X 3 Find F G X Brainly Com




F R R G R R F X X 1g X 2x 3 Find F G F G F G Maths Relations And Functions Meritnation Com
We see that mathf(0)=0 \dots /math Let us derive the two sides of the given equality math2 f'(2x)=2x1/math But, we have that mathf(2x)=x^2x \quad \Rightarrow \quad x=f(2x)x^2/math So, we can obtain the following ODE mathg^{'} =F(x) = (2x3)/(x4), g(x) = (4x3)/(2x)When we reverse the order the result is rarely the same So be careful which function comes first Symbol The symbol for composition is a small circle (g º f)(x




Functions Limits And Continuity




B Let F X 2x 3 G X 3x 4 And H X 4x For X R Where R Is Set Of Real Numbers Find Gof Fo8 Foh And Goh Answer Discrete Structure




Find The Remainder When F X X 3 6x 2 2x 4 Is Divided By G X 3x 1 Youtube
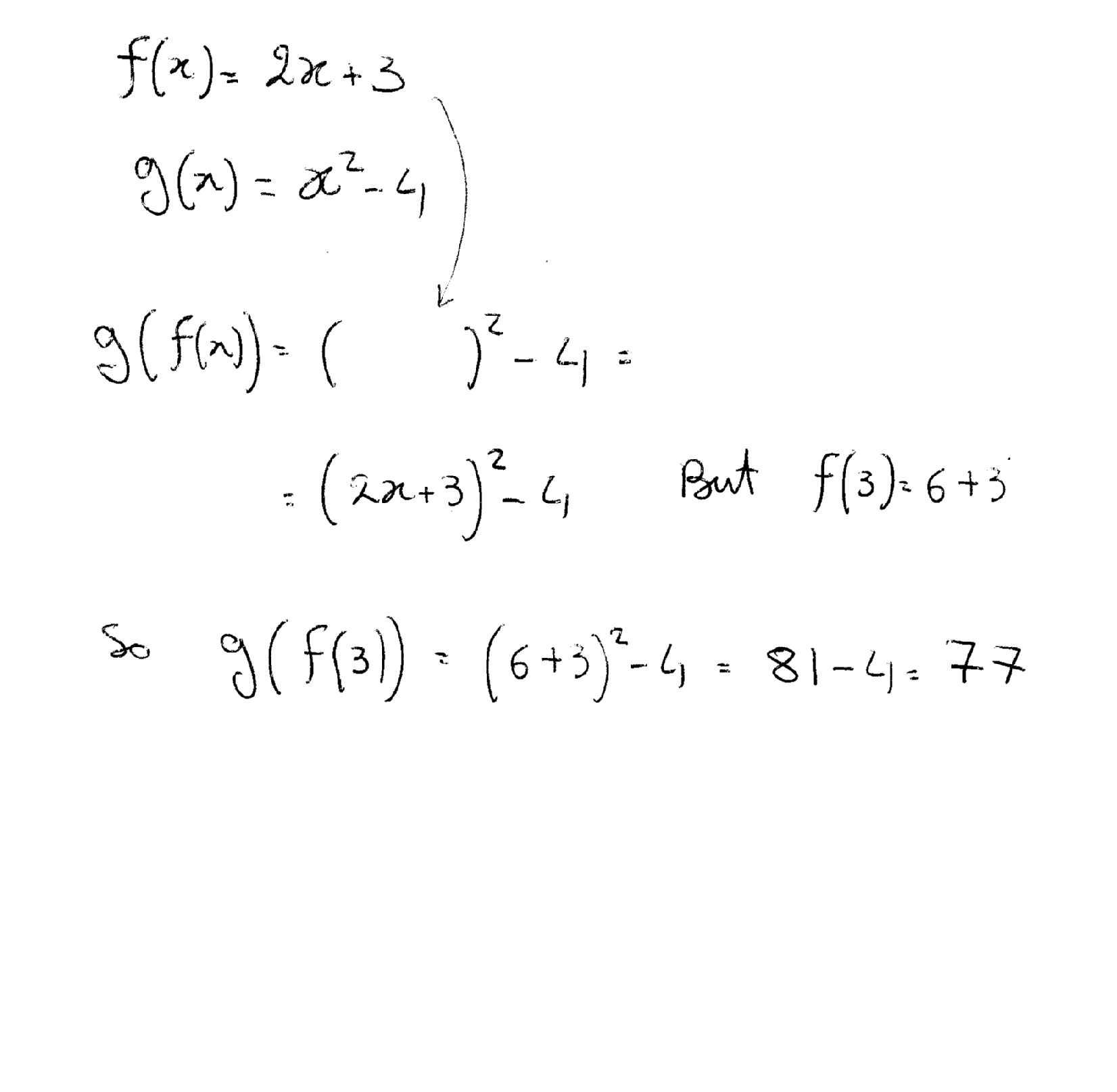



Let F X 2x 3 And G X X 2 4 And H X X 3 2 How Do You Find G F 3 Socratic



Math Scene Equations Iii Lesson 3 Quadratic Equations
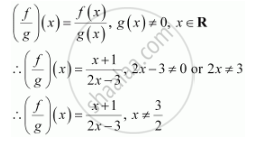



Let F G R R Be Defined Respectively By F X X 1 G X 2x 3 Find F G F G And F G Mathematics Shaalaa Com




Let F R To R F X 2x 3 And G R To R G X 1 2 X 3 Show That Youtube




If F X 2 X 3 G X X 3 X 4 And H X 2 2x 1 X 2 X 12 Then Find Lim Xrarr3 F X G X H X




Find The Following F X 2x 3 G X 2 X F Chegg Com




Answered F X 2x 1 And G X X 9 2 A F O Bartleby



Search Q Composite Functions Tbm Isch




Consider F X 7x 1 G X X3 Consider Fog Der Chegg Com



Write Up 1 By Amanda Oudi




Misc 7 Let F X X 1 G X 2x 3 Find F G F G F G



Http Www Humbleisd Net Cms Lib2 Tx Centricity Domain Algebra of functions and composite functions Pdf




Ged 18 Let F X X G X Vin X In X Tion By H X Log 0 5x 4x2 4x 3 X2 2x 3 Where X X Represent Fractional Function And Greatest Integer Function Then 1




1 Functions




Example 16 Let F X X2 And G X 2x 1 Find F G Fg F G



Solution If F X 2x 1 And G X X 2 Find 1 G G X 2 G F X 3 F G X 4 F F X
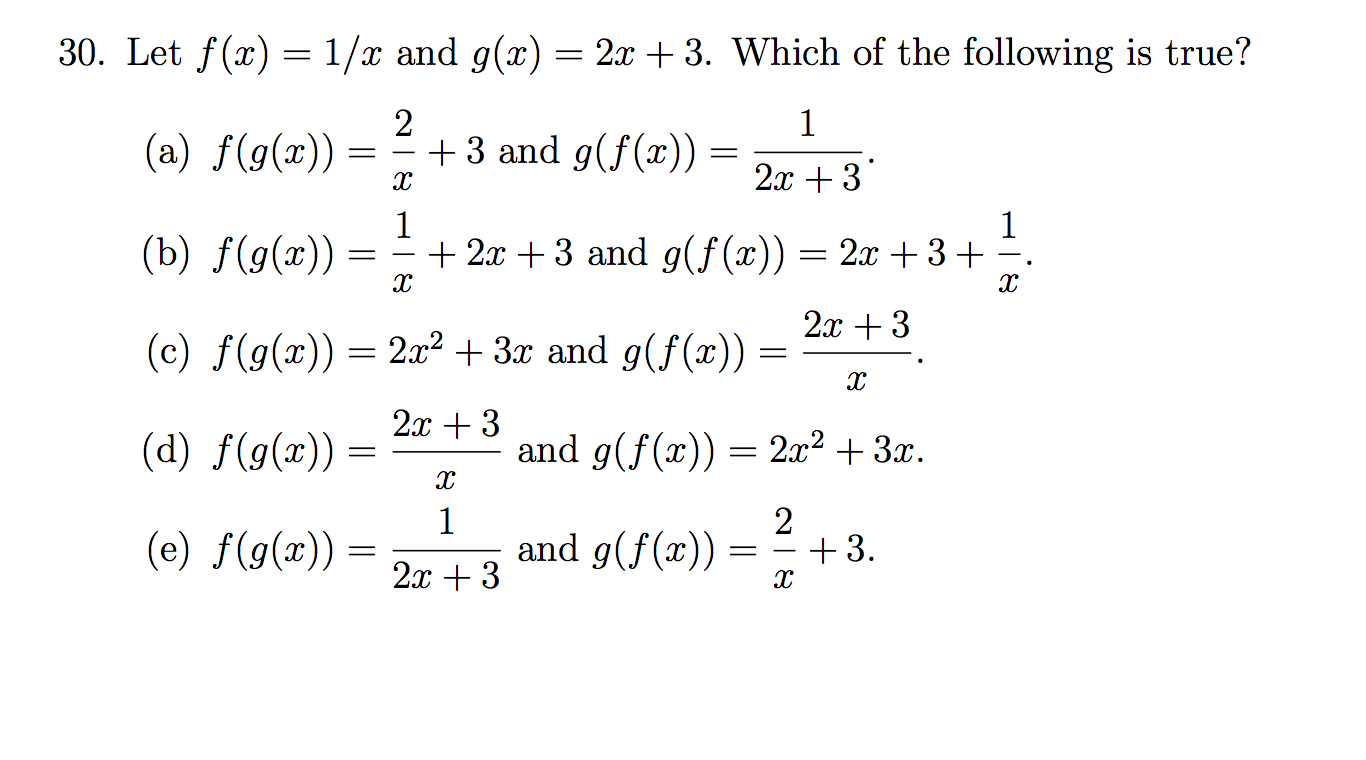



Let F X 1 X And G X 2x 3 Which Of The Chegg Com




Let F X 2x 2 X 1 And Let G X X 1 Which Statement Is True Brainly Com




If F X Sqrt 2 X And G X Sqrt 1 2x Then The Domain Of Fog X Is Youtube



F O G 2



How Do You Find The Area Between F X X 2 2x 1 G X 3x 3 Socratic



What Must Be Added To F X 4x 4 2x 3 2x 2 X 1 So That The Resulting Polynomial Is Divisible By G X X 2 2x 3 Sarthaks Econnect Largest Online Education Community




7 If F X And G X X2 2x Find Fg X And Its Chegg Com



View Question Math




Help Me If F X X 2 1 And G X 2x 3 What Is The Domain If F G X Brainly Com




For F X X 1 3 And G X 1 2x Find The Chegg Com




Use The Graph That Shows The Solution F X G X F X 3 4x 2 3x 1 G X 2 X What Is The Brainly Com




Let F X X 2 And G X 2x 1 Be Two Real Functions Find F G X F G X Fg Youtube




If F X 2x 3 G X 1 2x And H X 3x Prove That F O G O H F O G O H



What Must Be Added To F X 4x4 2x3 2x2 X 1 So That The Resulting Polynomial Is Divisible By G X X2 2x 3 Snapsolve




Let F G R R Be Defined Respectively By F X X 1 G X 2x 3 Find F G F Gand F G




Verifying Inverse Functions By Composition Not Inverse Video Khan Academy




Given That F X 2 X 4 And G X 3 X 5 Find Gf 3 With Noob Like Steps Please I Need A Really Clear Working To Fully Understand Thanks 3 Socratic




Additional Mathematics Functions Questions 1 Given Function F X Mx 4 X N X N If F 2 10 And F 8 4 Find A The Values Of M And N B The Ppt Download




If F X 2x 3 And G X X 6 Use The Graph To Find The Solution To The Equation F X Brainly Com




Lesson 1 1 Pages 5 11 State The Domain And Range Of Each Relation Then State Whether The Relation Is A Function Write Yes Or No Pdf Free Download




Given That F X X 2 2x 3 Find The Value S For Chegg Com
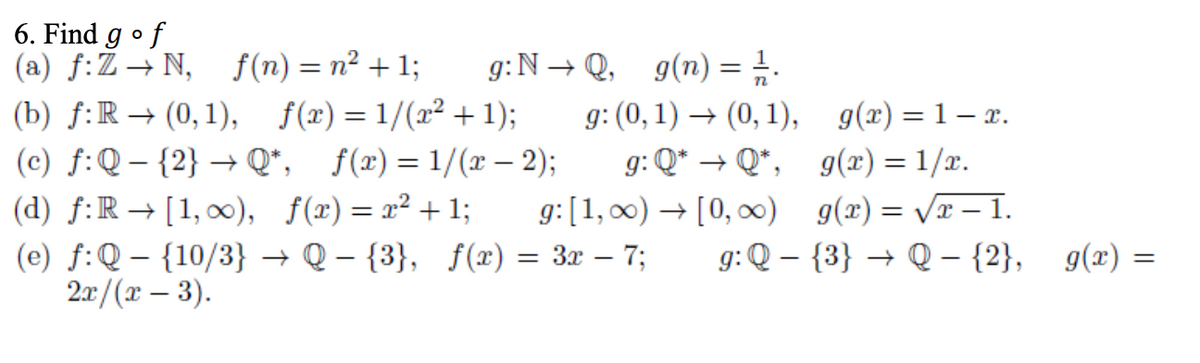



Answered Find G Of A F Z N B F R 0 1 Bartleby



Given F X X 2 2x 3 And G X 1 2 X Math Homework Answers




Solve 1 X 5 2 X 2 X 3 4 108 X 3 4 27 X 5 2 2 5 32 2 5 X 2 3 9 X 2 2 X 32 1 5 2 X 4 X 2 3 3 2 9 3 2 Ppt Download



Www Fairviewhs Org Staff Scott Myers Classes Precalculus Files




The Function Fand G Are Defined By Fx X 3 1 G Gauthmath




F X 2x 3 5x 2 7x 3 And G X 2x 3 What Is The Quotient And Remainder In The Form Q X R X G X Socratic




F X Sqrt X G X 2x 3 Youtube
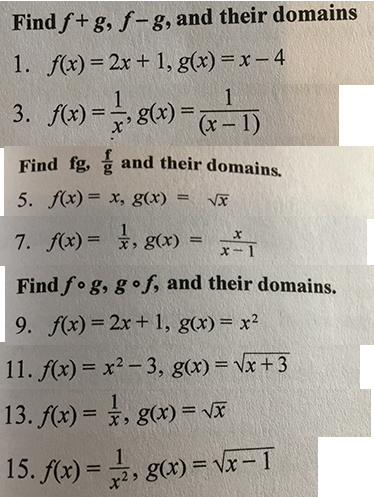



The Questions Are All Odd Numbers 1 3 5 7 9 11 Chegg Com




If F G Rvecr Are Defined Respectively By F X X 2 3x 1 G X 2x 3 Find Fog Ii Gof Iii Fof Iv Gog




Let F G R R Be Defined Respectively By F X X 1 G X 2x 3 Find F G F G And F G




Algebra Ii Operations On Functions




Wolfram Alpha Examples Step By Step Solutions




If F X 3x 1 And G X X 2 Find F G X Brainly Com




If F X Sqrt X 2 1 G X X 1 X 2 1 And H X 2x 3 Then Find F Prime H Prime G Prime X




Function Composition Given F X 2x 2 And G X 2 Find F ºg X F ºg X F G X Start On The Inside F G X G X 2 So Replace It F G X F 2 Ppt




Answered Given F X 2x 3 And G X X 1 Bartleby




If F X 2x 3 G X X 3 5 Then Find Fog And Show That Fog Is



Solved Given That F X 2x 3 And G X 9x 2 5x 11 Determine The Following Course Hero



Math Scene Equations Iii Lesson 3 Quadratic Equations




If F X 2x 3 G X X 3 5 Then Find Fog And Show That Fog Is




Given That G X 3x 2 2x 1 Find Each Of The Following A G 0 B G 1 C G 3 D G X Brainly Com




Ex 1 5 Aster Classes



Http Smacmathapcalculus Weebly Com Uploads 1 9 2 5 Fc Unit 3 1 Hw Key V2 Pdf
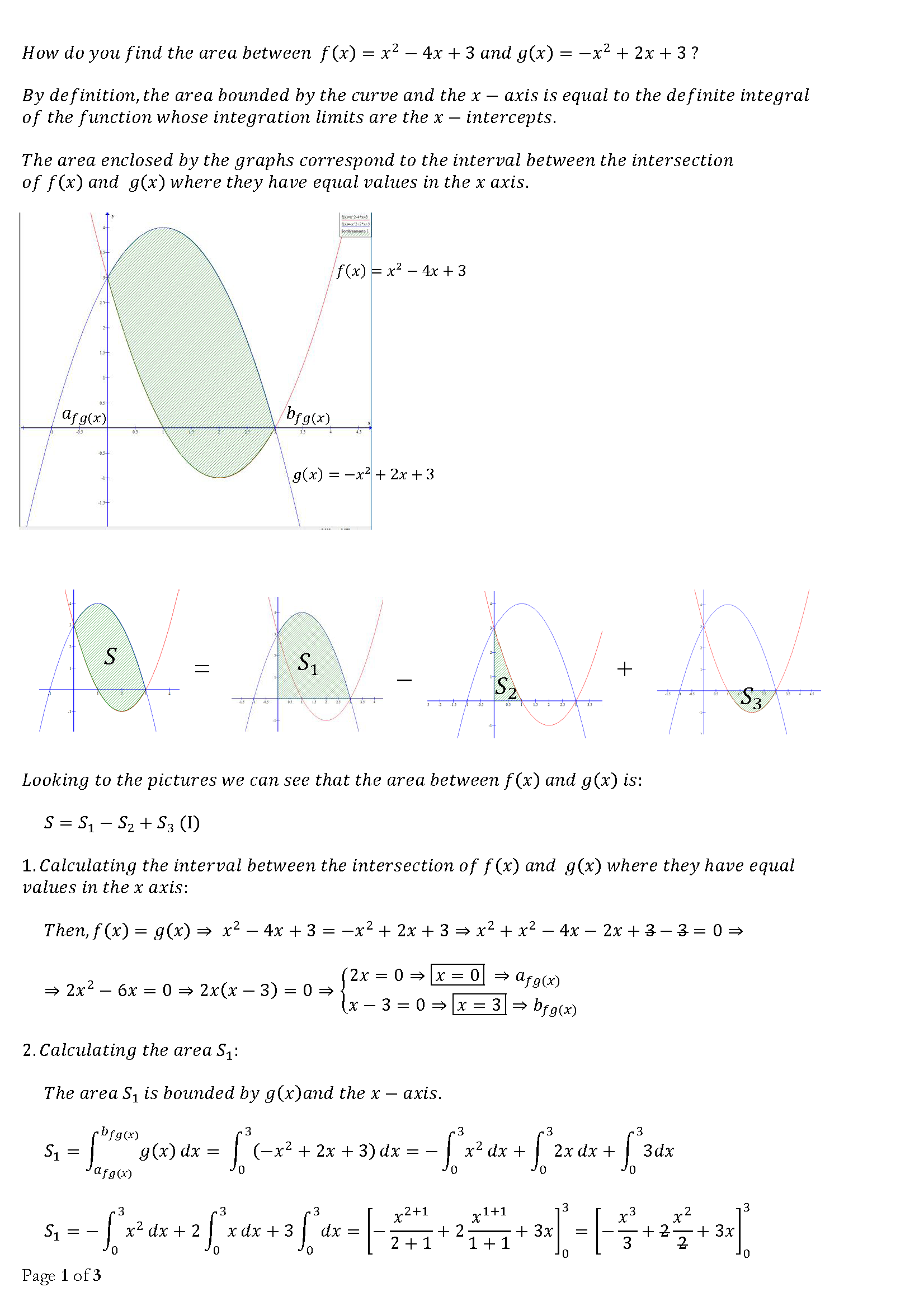



How Do You Find The Area Between F X X 2 4x 3 And G X X 2 2x 3 Socratic




If F G R R Are Defined By F X X2 3x 1 G X 2x 3 Find Fog Maths Relations And Functions Meritnation Com




2 Let F X 2x 3 And G X X 4 X In R Find The Following 1 Fof 1 Ii Fog 1 Iii Youtube




Given F X 3x 1 And G X 2x 3 For Which Value Of X Does G X F 2 Brainly Com



If F X 2x 2 And G X 1 3x Then Fog Is 1 3 2x 2 2 2 3x 2 3 2 9x 2 4 1 6x 2 Sarthaks Econnect Largest Online Education Community
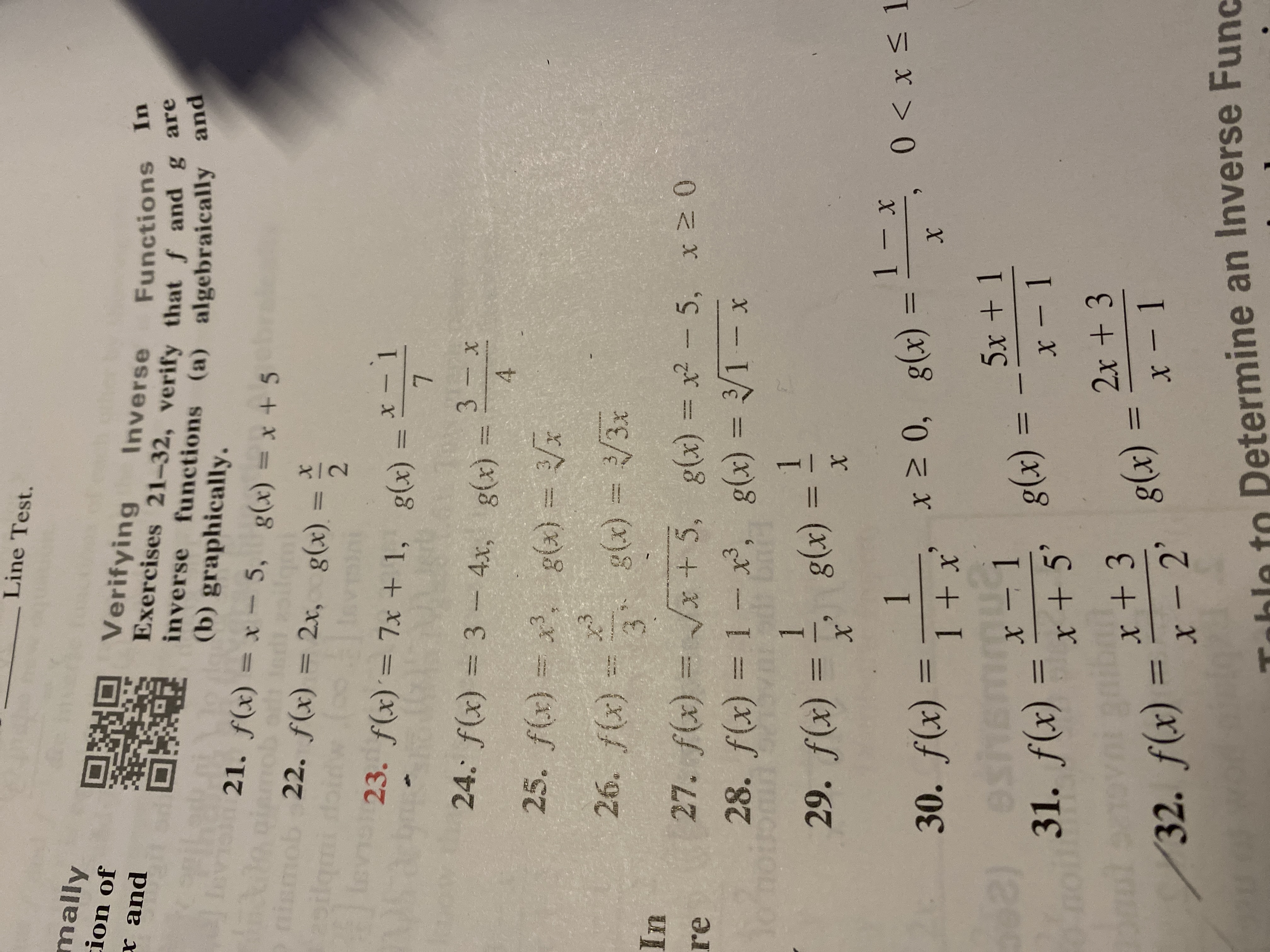



Answered 32 F X X 3 2x 3 G X X 1 ニ ニ Bartleby




If The Function F R R Be Defined By F X 2x 3 And G R R By G X X3 5 Then Find The Value Of Fog 1 X Dronstudy Questions




View Question 1 Graph Both Functions To Find The Solution S To The System Thanks For All Your Help
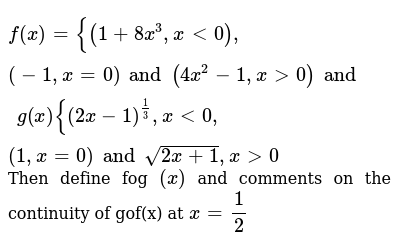



Give F X 2x 3 G X 1 2x And H X 3x Prove That Fo Goh Fog Oh



Http Www Cusd80 Com Cms Lib6 Az Centricity Domain 2148 Q1 exam review 13 14 key pdf Pdf



Www Sd308 Org Cms Lib8 Il Centricity Domain 3273 Section 6 1 practice answers Pdf



F O G Math



Search Q F O G X Tbm Isch




Given That F X 3x 1 G X 5x 8 And H X 2x Homeworklib



Math Scene Equations Iii Lesson 3 Quadratic Equations



0 件のコメント:
コメントを投稿