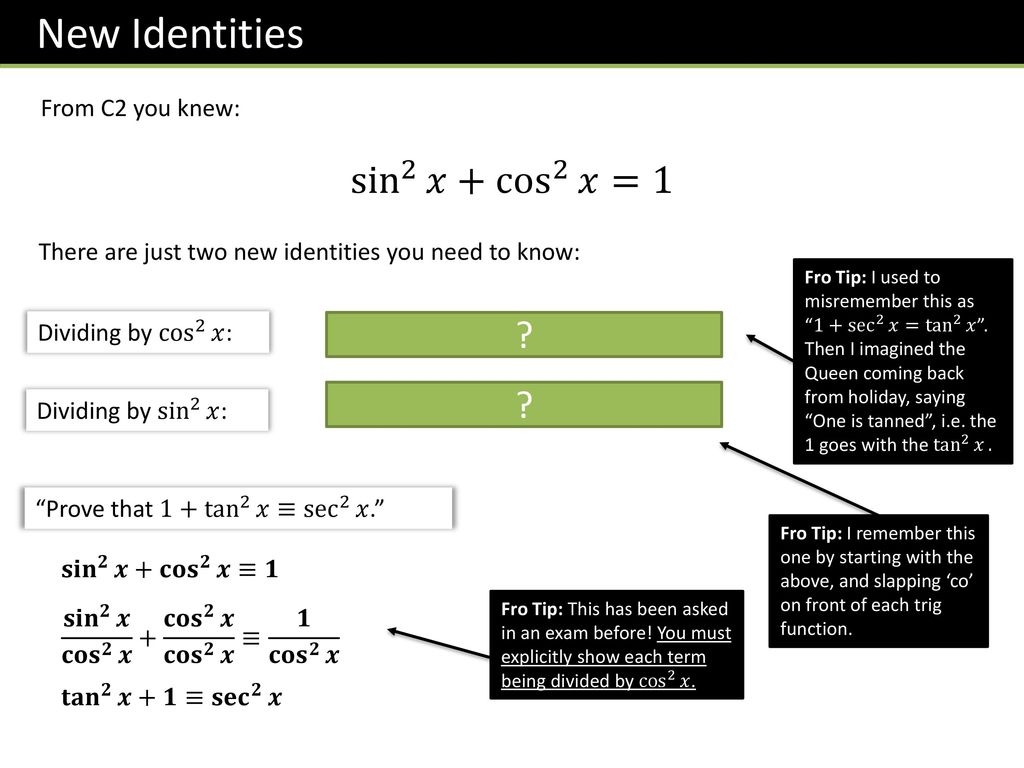
sin^2 (x) cos^2 (x) = 1 everywhere An alternate approach to proving this identity involves using the "unit circle" (radius = 1) Since the radius isSince tanθ = sinθ cosθ and secθ = 1 cosθ , ⇒ tan2θ 1 = sec2θ Hence Proved cos(x − x) = cos2x sin2x = 1 then divide by cos2x to get the result above I've assumed the one of the trigonometric results d dθ(1 tan2θ) = 2tanθsec2θ d dθsec2θ = 2secθ(tanθsecθ) = 2tanθsec2θ Thus (1 tan2θ) − sec2θ is a constantI know that and The next step would then be to say that but now what?
Answered Prove The Identity 1 Tanx Sec 2x 2 1 Bartleby
1+tan^2x=sec^2x proof
1+tan^2x=sec^2x proof-Dividing the numerator and denominator by $\cos x$ gives $$\frac{\sin x \cos x}{\cos x \sin x} = \frac{\tan x 1}{1 \tan x},$$ and then observe that $\tan \frac{\pi}{4} = 1$ Then recall the tangent addition identity $$\tan(\alpha \beta) = \frac{\tan \alpha \tan \beta}{1 \tan \alpha \tan \beta}$$ For what suitable choices of Using the following tan(x) = sin(x)/cos(x) cos^2(x)sin^2(x) = 1 sec(x) = 1/cos(x) for cos(x)!=0, we have 1tan^2(x) = cos^2(x)/cos^2(x) (sin(x)/cos(x))^2 =cos^2(x)/cos^2(x)sin^2(x)/cos^2(x) =(cos^2(x)sin^2(x))/cos^2(x) =1/cos^2(x) =(1




Trig Identity Sec 4x Tan 4x 1 2tan 2x Youtube
Tanx = t Sec^2 x dx= dt So now it is, 1/(1t)^2 dt This integral is given by 1/1t and t= tanx So, it is cosx/cosx sinx Integral of the function \frac{\cos ^2 x}{1\tan x} Integral of the function 1Tan^2x sec^2x = 1, 1 See answer baneenbilal8480 is waiting for your help Add your answer and earn pointsAll these good answers are algebraic proof If we want to visualize this whole thing geometrically(And if computer has to draw the picture and proof without human intervention) then GeometrifyingTrigonometry which is a part of Geometric Automata
Yes, sec 2 x−1=tan 2 x is an identity sec 2 −1=tan 2 x Let us derive the equation We know the identity sin 2 (x)cos 2 (x)=1 ——(i) Dividing throughout the equation by cos 2 (x) We get sin 2 (x)/cos 2 (x) cos 2 (x)/cos 2 (x) = 1/cos 2 (x) We know that sin 2 (x)/cos 2 (x)= tan 2 (x), and cos 2 (x)/cos 2 (x) = 1 So the equation (i) after substituting becomes Ex 34, 8 Find the general solution of the equation sec2 2x = 1 – tan 2x sec2 2x = 1 – tan 2x 1 tan2 2x = 1 – tan2x tan2 2x tan2x = 1 – 1 tan2 2x tan2x = 0 tan 2x (tan2x 1) = 0 Hence We know that sec2 x = 1 tan2 x So, sec2 2x = 1 tan2 2x tan 2x = 0 taSeparate fractions Rewrite tan(x) tan ( x) in terms of sines and cosines Multiply by the reciprocal of the fraction to divide by sin(x) cos(x) sin ( x) cos ( x) Convert from cos(x) sin(x) cos ( x) sin ( x) to cot(x) cot ( x) Divide sec2(x) sec 2 ( x) by 1 1 Rewrite sec(x) sec ( x) in terms of sines and cosines
Trig identity $1\tan x \tan 2x = \sec 2x$ Ask Question Asked 10 years, 1 month ago Active 5 years, 11 months ago Viewed 6k times 3 0 $\begingroup$ I need to prove that $$1\tan x \tan 2x = \sec 2x$$ I started this by making sec 1/cos and using the double angle identity for that and it didn't work at all in any way everMath\left { \quad \dfrac { 1 2 \sin ^ { 2 } x } { 1 \sin 2 x } } \\ { =\dfrac { \cos ^ { 2 } x \sin ^ { 2 } x 2 \sin ^ { 2 } x } { \cos ^ { 2 } x \sinTo do this one we need the identity and its rearranged version Factor common factor out of the left side Replace the first
.JPG)



Every Day I M Calculatin I D3 Unit Q Pythagorean Identities




Sin2x Secx 1 Sec2x Sec2x 1 Brainly In
Prove that 1/sin thetatan theta and 1/cos theta = 1/cos theta and 1/sec thetatan theta integral confusion integral of Sec2xTan2x i know u is sec 2x du=2sec2xtan2x dx what would i have to multiply with du so it would equal tan 2x dx?Prove that (1cot^2x)tan^2x = sec^2xSolution we have to prove tan^2x(cos^2x1)Cos^2x=Sec^2x consider left hand side tan^2x(cos^2x1)Cos^2x tan^2x = sin^2x /cos^2x plug in above ( sin^2x /cos^2x )(cos^2x1)Cos^2x



Prove Each Identity C Frac 1 Sin 2xcot 2x 1 Cos 2x Gauthmath




Use A Similar Line Of Reasoning To Prove That 1 T Gauthmath
Are there any greater risks of traveling significantly faster to another planet? Starting from cos2(x) sin2(x) = 1 Divide both sides by cos2(x) to get cos2(x) cos2(x) sin2(x) cos2(x) = 1 cos2(x) which simplifies to 1 tan2(x) = sec2(x) Answer linkVerify the Identity cot (x)^2 (sec (x)^21)=1 cot2 (x) (sec2 (x) − 1) = 1 cot 2 ( x) ( sec 2 ( x) 1) = 1 Start on the left side cot2(x)(sec2(x)−1) cot 2 ( x) ( sec 2 ( x) 1) Apply pythagorean identity cot2(x)tan2(x) cot 2 ( x) tan 2 ( x) Convert to sines and cosines Tap for more steps Write cot ( x) cot ( x) in sines and cosines




Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco



Solved Prove The Following Trigonometric Identity Tan 2x Tan X Sec 2x 1 For Each Step Of Your Proof Include A Written Rationale And Or Indi Course Hero
Solve The posistion of a particle moving along a coordinate line is s=sqrt(54t), with s in meters and t in seconds Find the particle's velocity at t=1 sec A) 2/3 m/sec B) 4/3 m/sec C) 1/3 m/sec D) 1/6 m/sec Thank you! Find an answer to your question tan^2x 1 = sec^2x PROVE hopelafave hopelafave Math Secondary School answered Tan^2x 1 = sec^2x PROVE 1 See answer hopelafave is waiting for your help Add your answer and earn points`1tan^2x = sec^2x` `1cot^2x = cosec^2x`



Solved Solve The Following A Find The Exact Measures Of The Angle Theta Where Theta 2 Pie 10sec Degree 2 18 B The Height Of A Nail I Course Hero




Trigonometric Identity In Double Angle Sin2x Cos2x 1 Sin2x Cos2x 1 Sec2x Tan2x Youtube
$\tan^2x \sec^2x$ express in terms of sin/cos 18 Is there objective proof that recent bills (1st half of 21) that restrict voting are targeting Democratic voters specifically?You could take tan(x) out of the fraction, but I still don't know how to go about simplifying it The book says the answer is1 Tan 2x Sec 2x Proof bayern paris champions league bayern trikot 15 16 bayern spiel heute abend bayern vs dortmund 6 0 bayern münchen spielplan 19 bayern münchen sc freiburg bayern münchen training säbener straße bayern vs dortmund 18 19 Proof Tan 2 1 Sec 2 Youtube




How Many Can You Derive From First Principles Ppt Download




Prove That Sec8x 1 Sec4x 1 Tan8x Tan2x
Answers 15,878 km 7,761 km 422 km 262 km We'reIf my question is confusing, then here's another example of what i'm talking about integral of (3x(sec^2x1)(csc^2x1)=1 prove the following identity ive been stuck on this for hours please help Trigonometry For all values of x for which the expressions are defined, prove the following equation identity 2/sec = 22 sin^2 x/ cos x Trigonometry Simplify each expression using the




Verifying A Trigonometric Identity Tan 2 X 1 Sec X Sec X Youtube



P2 Chapter 6 Trigonometry Ppt Download
Math Find sec θ and csc θ If tan θ =3 and cos θ>0 Please helpp, i don't get identities MathsSs triG Tan^2x1=sec^2x proof Tan^2x1=sec^2x proof tan^2 x1=sec^2x So to get 1 on the other side of the equal sign wouldn't it be sec^2xtan^2x=1?Verify (1tan^2x)/(1cot^2x) = 1sec^2x Answered by a verified Math Tutor or Teacher We use cookies to give you the best possible experience on our website By continuing to use this site you consent to the`(1tanx )^2 (1cotx )^2 ` `= 12tanxtan^2x12cotxcot^2x` `= (1tan^2x)(1cot^2x)2(tanxcotx)` We know that;




Sec 2 2x 1 Tan2x Youtube



Solved Verify Each Identity Solve As A Two Column Proof Chegg Com
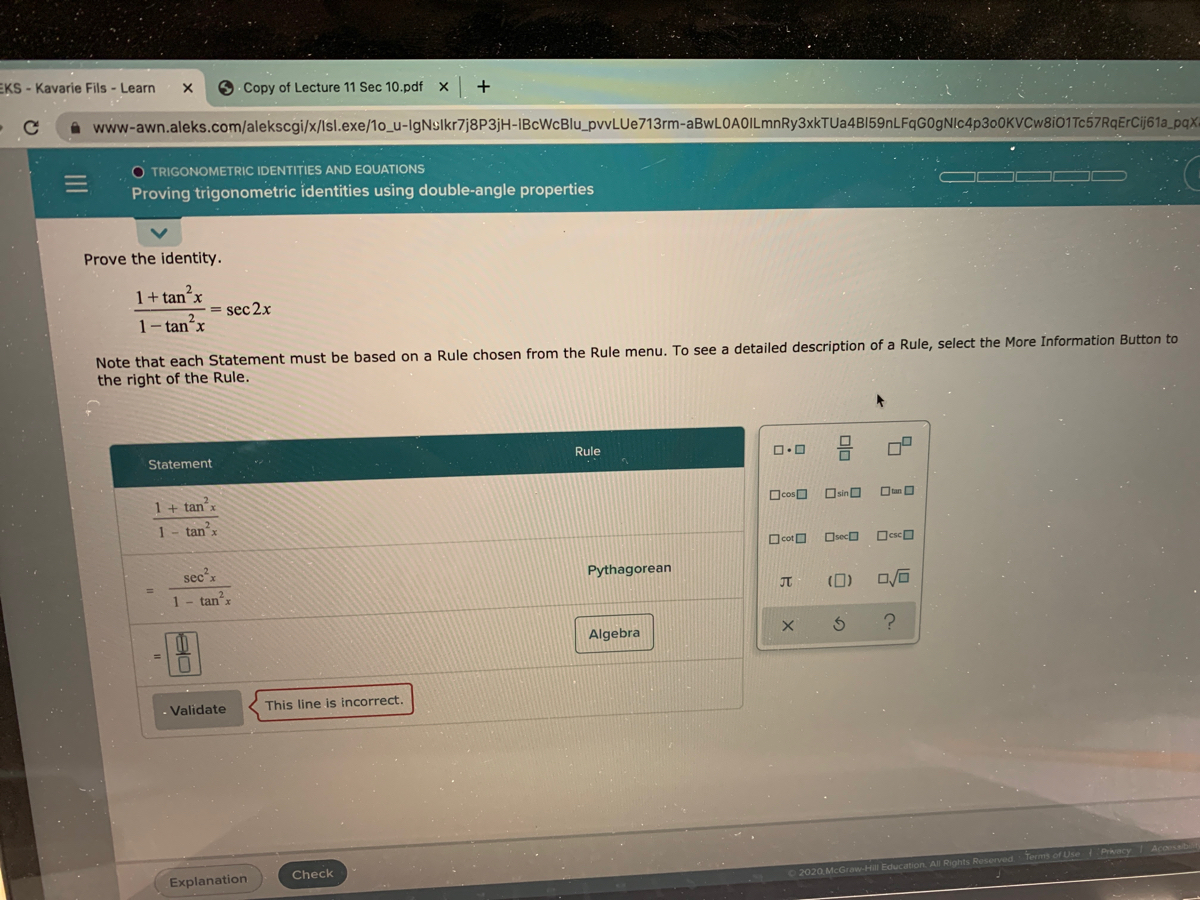
Ex 34, 8 Find the general solution of the equation sec2 2x = 1 – tan 2x sec2 2x = 1 – tan 2x 1 tan2 2x = 1 – tan2x tan2 2x tan2x = 1 – 1 tan2 2x tan2x = 0 tan 2x (tan2x 1) = 0 Hence We know that sec2 x = 1 tan2 x So, sec2 2x = 1 tan2 2x tan 2x = 0 taComplete the proof of the identity by choosing the Rule that justifies each step cosx (1 tan 2x)secr To see a detailed description ofWeekly Subscription $199 USD per week until cancelled Monthly Subscription $699 USD per month until cancelled Annual Subscription $2999 USD per year until cancelled User Data Missing Please contact support We want your feedback (optional) (optional) Please add a message Message received Thanks for the feedbackIn this video I go over the proof of the trigonometry identity tan^2(x) 1 = sec^2(x) The proof of this identity is very simple and like many other trig id




The Expression 1 Tan X Tan 2 X 1 Cot X Cot 2 X Has The Positive Values For X Given By




How Many Can You Derive From First Principles Ppt Download
Get an answer for 'verify (1 tan^2x)/(tan^2x) = csc^2x' and find homework help for other Math questions at eNotes Verify the identity `1/(tan^2x) 1/(cot^2x) = csc^2x sec^2x` 22tanx/1tan^2x YOU MIGHT ALSO LIKE Reciprocal, Quotient, and Pythagorean Identities 8 terms jessgac00 Trigonometric Identities some 35 terms baaskat000 trigometric identities StartSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreTan^2x sec^2x = 1, baneenbilal8480 baneenbilal8480 Mathematics High School answered Prove this trigonometric equation;




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic
You can put this solution on YOUR website! not sure how to start this one, i have tried it a few different ways and i still can't get it (1 tanx)^2 = sec^2x 2tanx1 Tan 2x Sec 2x Proof dark paranoia quotes deadlight director s cut
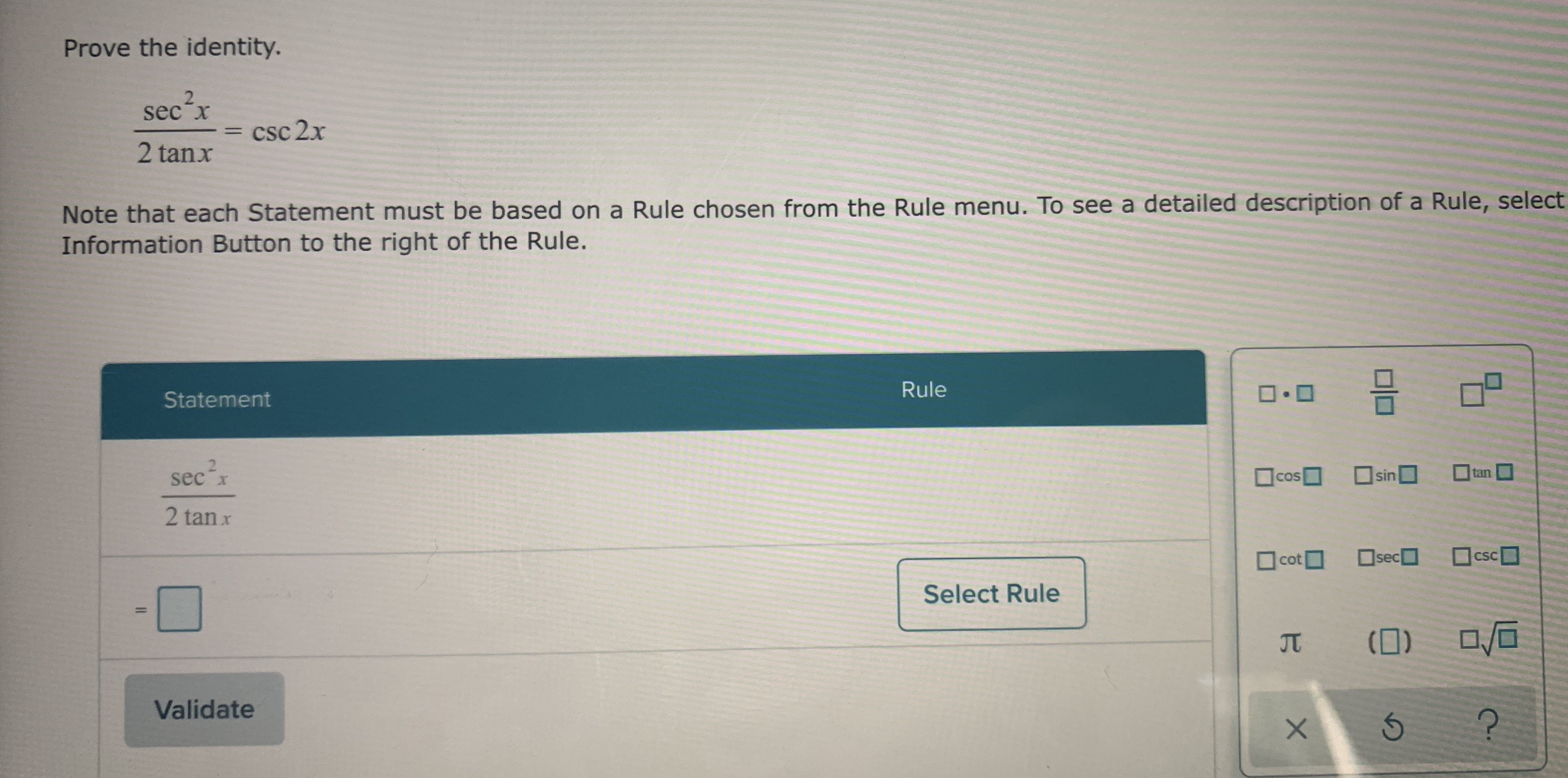



Answered Prove The Identity Sec X Csc 2x 2 Tanx Bartleby




1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube
👍 Correct answer to the question Prove that tan^2x sec^2x=1 eeduanswerscomSolution for prove that 1 tan 2x = sec 2x Social Science Anthropology Prove that tan 2 (x) 1 = sec 2 (x) Prove that tan 2 (x) 1 = sec 2 (x) We know that sin 2 (x) cos 2 (x) = 1 dividing both sides by cos 2 (x) we get (sin 2 (x) cos 2 (x))/cos 2 (x) = 1/cos 2 (x) which equals sin 2 (x)/cos 2 (x) cos 2 (x)/cos 2 (x) = (1



Www2 Math Binghamton Edu Lib Exe Fetch Php People Mckenzie Trig Identities Worksheet With Answers 2 Pdf




Find The Derivative Of The Given Function Y Tan 2x 1 Cot 2x I Tried Converting The Original Function In Terms Of Sin And Cos But It Was Still Too Complicated To Be Called Simplified
Prove 1tan^2x=sec^2x using triangles Prove 1tan^2x=sec^2x using trianglesFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor0603 Prove 1tan^2x = sec^x anarkha1111 is waiting for your help Add your answer and earn pointsWeekly Subscription $199 USD per week until cancelled Monthly Subscription $699 USD per month until cancelled Annual Subscription $2999 USD per year until cancelled User Data Missing Please contact support We want your feedback (optional) (optional) Please add a message Message received Thanks for the feedbackPhysics A record for a marathon is 0h, 900min, 210 sec If the average speed of a runner achieving this record is 5436 m/s, what is the marathon distance?




Prove That Sec 2x Cosec 2x Tan 2x Cot 2x




Trig Identity Tan X 1 Tan 2 X Sec X Cos X Csc X Sin X Proved From Both Sides Youtube
Prove that tan^2x sec^2x =1 9,072 results, page 17 Math The height of a ball t seconds after it is thrown upward from a height of 6 feet and with an initial velocity of 80 feet per second is f (t) = 16t^2 80t 6 According to Rolle's Theorem, what must beProve that tan^2x sec^2x =1 9,060 results, page 61 precalculus Prove m∠ABC = 123 How do I write this in a two column proof? Click here 👆 to get an answer to your question ️ prove this trigonometric equation;



What Is The Derivative Of Tan 1 Sec X Tan X Quora




Prove Or Disprove The Identity If You Find The Identity Is True State The First Line Of The Proof Brainly Com
Verify sec2x tan2x = (1 − sin4x)sec4x My solution sec2x tan2x = 1 cos2x sin2x cos2x = 1 sin2x cos2x = 1 sin2x cos2x ⋅ 1 − sin2x 1 − sin2x = 1 − sin4x cos2x ⋅ cos2x = 1 − sin4x cos4x = 1 cos4x − sin4x cos4x = sec4x − sin4xsec4x = sec4x(1 − sin4x) Is it incorrect to multiply in 1 − sin2x like in the fourthThe limits of those three quantities are 1, 1, and 1/2, so the resultant limit is 1/2 Proof of compositions of trig and inverse trig functions All these functions follow from the Pythagorean trigonometric identity We can prove for instance the function () =In this video, I go through a trigonometric proof which is1tan^2=sec^2The proof is fairly straight forward with some common knowledge of trigonometric fu



3



Www Rusdlearns Net C File Show
Here is what I have from Chri H that I could use for my own proof 1 tan 2x sec 2x Another identity that is used quite a bit especially in calculus involving trigonometric functions 9 years ago sec2x tan2x 1—–Now sin2xcos2x 1 IDENTITY Follow edited Jan 17 13 at 644




Prove That Tan Pi2 X Sec Pi X Sin X Sin Pi X Cot 2pi X Pi2 X 1




If Sec X Tan X A Then A 2 1a 2 1




The Derivative Of Tan X Is Sec 2 X Why Mathematics Stack Exchange




Prove The Following Identities If It Is A One Step Chegg Com




How Do You Simplify Sec 4x Tan 4x Sec 2x Tan 2x Socratic




Example 7 Show That Tan 1 X Tan 1 2x 1 X2 Inverse



1



Tan 2x Tan 2x




Trig Identity Sec 4x Tan 4x 1 2tan 2x Youtube



Solved Prove The Following Trig Identity Sec 2 X 2secx Cosx Cos 2 X Tan 2 X Sin 2 X Course Hero




How Does One Verify Cos 2x Sin 2x 1 Tan 2x Cos 2x Socratic




Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco




How Do You Prove Tan 2x Secx 1 1 Secx Socratic



Www Birmingham K12 Mi Us Cms Lib Mi Centricity Domain 976 Chapter 5 Pdf




Trig Identity Sec2x Minus Tan2x T10 Youtube




Iit 1994 Prove That Sec2x Tan2x Tan Pi 4 X When X Lies Between 0 And Pi 4 Youtube




Evaluate Lim Xrightarrow Frac Pi 2 Frac Tan 2x X Frac Pi 2 Orevaluate Lim Xrightarrow 3 Frac X 4 81 2x 2 5x 3 Snapsolve




Answered 8 In Parts A To E Simplify The Bartleby



How To Show That Sec X Tan X 1 Sec X Tan X Quora




Sec 6x Tan 6x 1 2 Tan 2x Sec 2x Important Difficult Trigonometric Identity Youtube
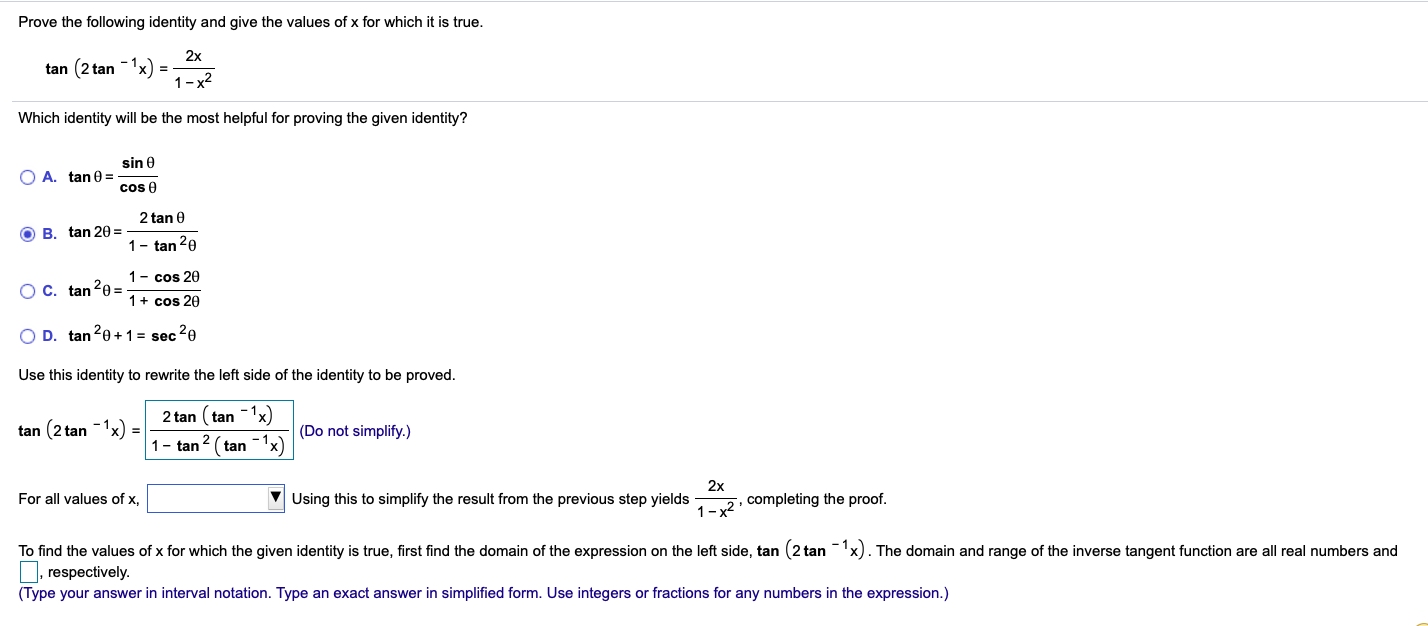



Prove The Following Identity And Give The Values Of X Chegg Com



Http Cneacs Weebly Com Uploads 2 4 8 5 3 Worksheet Sec 6 2 Sum And Difference And Double Angles Identity Worksheet Pdf




Basictrigonometry Pdf Trigonometric Functions Sine




If Tan X 2tan 2y 1 Then Show Cos2x Sin 2y 0 Z X And Deduce That Tan 750 T Tan X Tan 4 X Maths Trigonometric Functions Meritnation Com




Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf




How Do You Prove Tan 2x Secx 1 1 Secx Socratic




Answered Prove The Identity 1 Tanx Sec 2x 2 1 Bartleby




Tan2x Sec2x ただの悪魔の画像




Sin2x Cos2x 1 Proof




If Y Tan X Tan 2x Tan 3x Sin 12x 0 Then Dy Dx Has The Value Equal To



How Do You Prove Cosx Cscx 2sinx Tanx 1 Tan 2x Socratic




Prove Sec 4x Sec 2x Tan 4x Tan 2x




Prove That Derivative Of Tan X Is Sec 2 X By First Principle
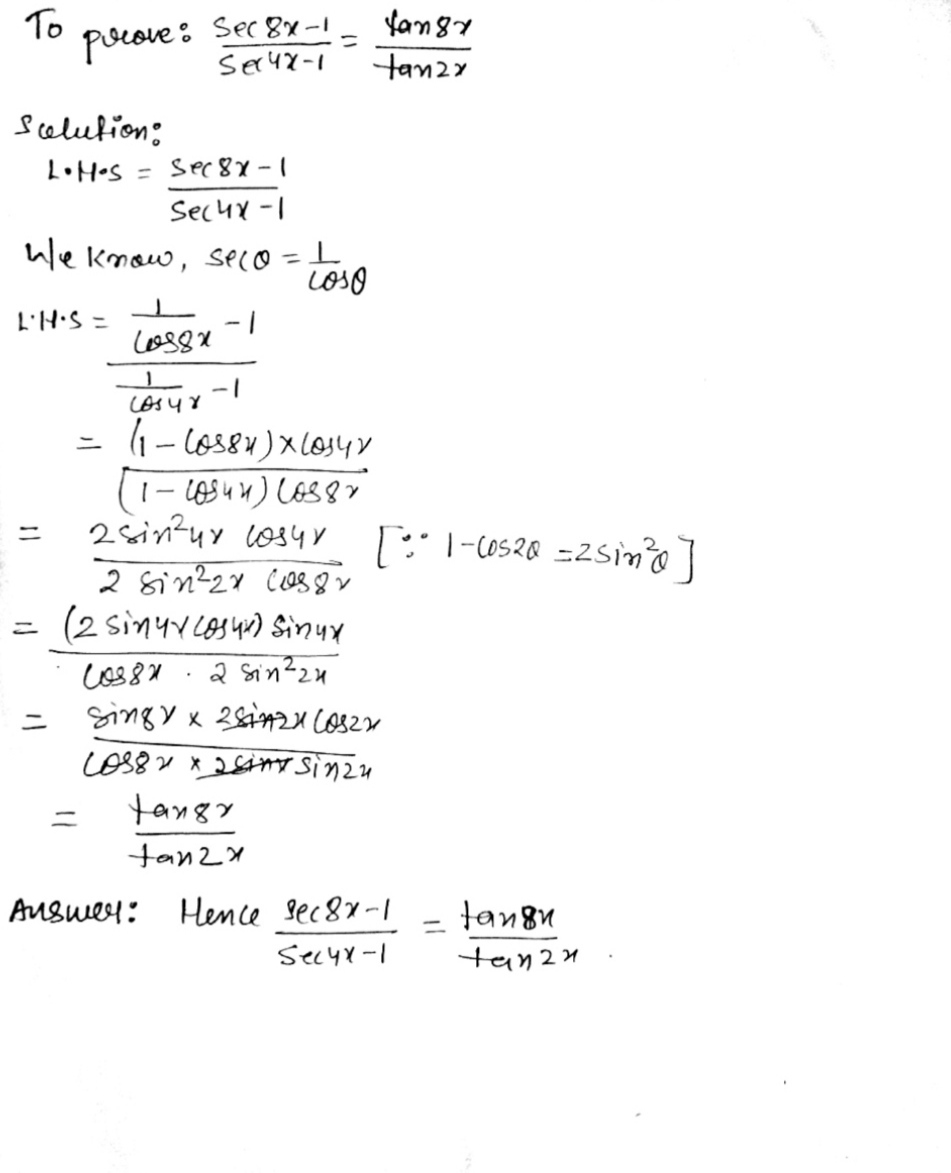



Prove That Frac Mathit Sec 8x 1 Mathit Sec 4x 1 Frac Tan 8x Tan 2x Snapsolve
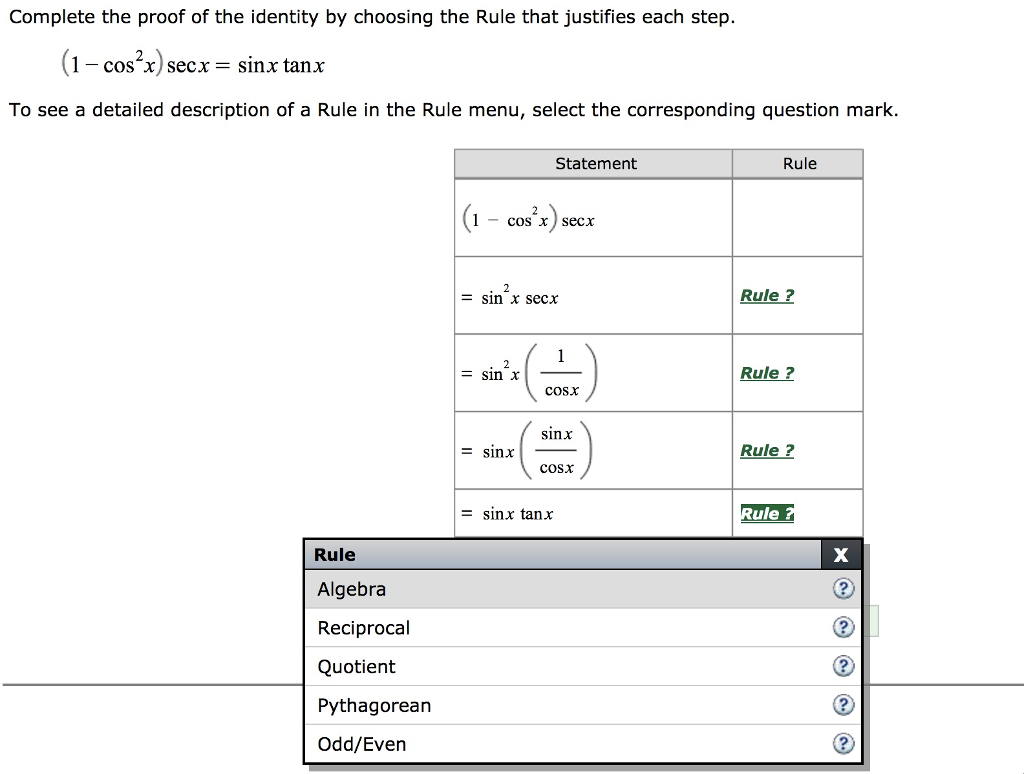



Complete The Proof Of The Identity By Choosing The Chegg Com



Derivative Of Tan X Old Video Khan Academy



Www Webassign Net Resources Bmcc Ch11 Pdf




Plzz Tell 30 2 30 Prove That Ii Tan 560 Cos110 Sin110 Cos 110 A Sin 110 I Maths Trigonometric Functions Meritnation Com




If Tan Theta Sec 2alpha Prove That Sin2theta 1 Tan 4alpha 1 Tan 4alpha




How Many Can You Derive From First Principles Ppt Download



Http Theprofessorshut Weebly Com Uploads 2 3 2 7 Pc Chap 6 Sect 2 Sum Difference And Cofunction Identities Pdf




Limit Trigonometric Function 2 Sec 2x 1 Tan X Youtube



Http Www Humbleisd Net Cms Lib2 Tx Centricity Domain 2966 Chapter 9 1 9 4 notes key Pdf



Prove The Identity Sec X 1 Tan X Tan X Secx 1 To Chegg Com




Ex 2 2 13 Inverse Trigonometry Tan 1 2 Sin 1 2x 1 X2




Prove That Tex Frac Sin 2x Sec X 1 Frac Sec 2x Sec 2x 1 Tan Frac X 2 Tex Brainly In




Prove The Following Identities I Sec 2x Tan 2xcos Gauthmath
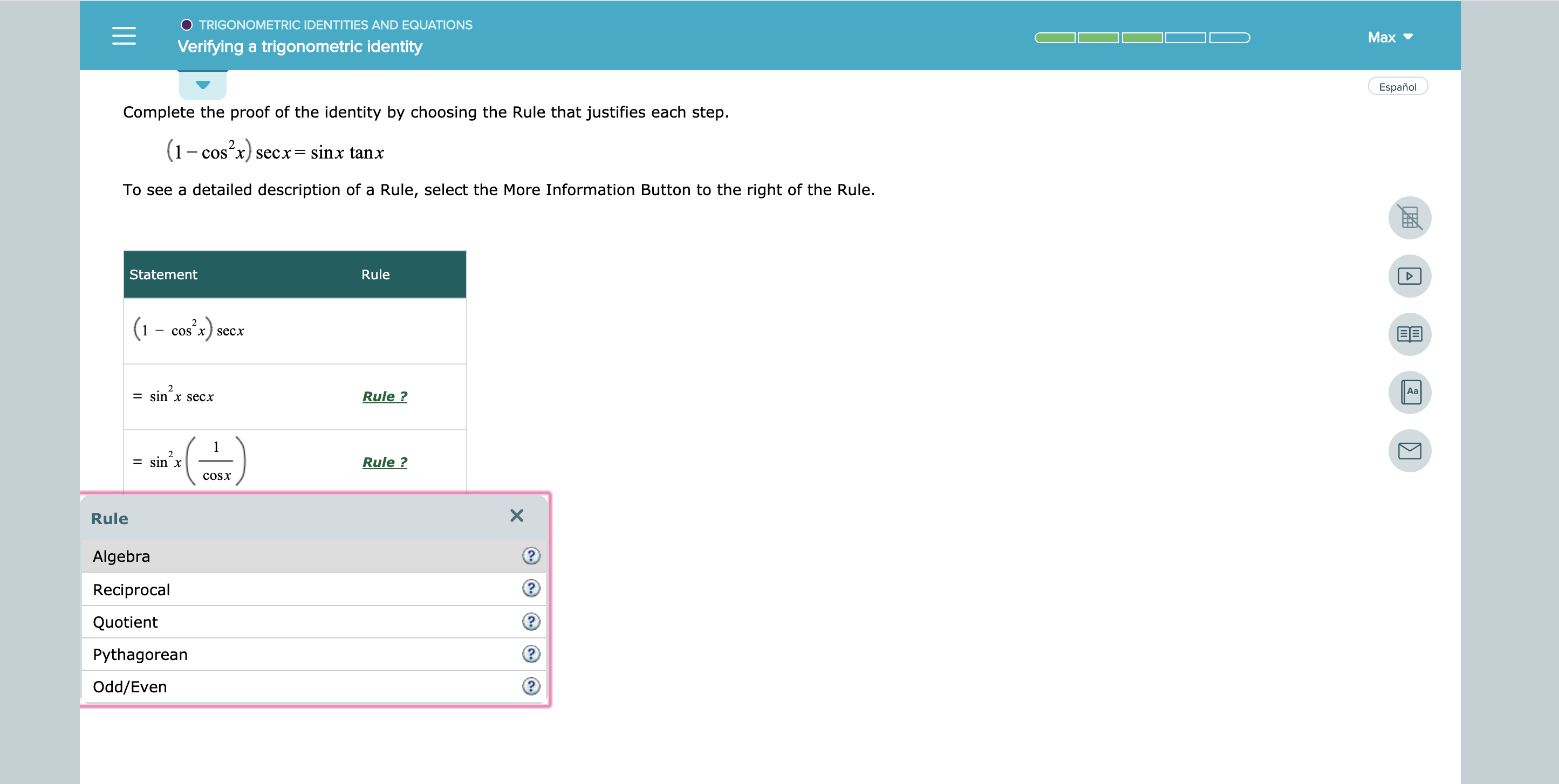



Answered Trigonometric Identities And Equations Bartleby




A Solution Of The Equation 1 Tan X 1 Tan X Sec 2x 2 Tan 2 0 Where X Lies In The Interval Pi2 Pi2 Is Given By




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Prove That Tan 2 2x Tan 2 X1 Tan 2 2x Tan 2 X Tan 3x Tan X




Solved Find Sin2x Cos2x And Tan 2x If Cosx And X Ter Chegg Com




1 Tanx Tan X 2 Secx Tanx Cotx 2 1 Prove It Brainly In



Mafiadoc Com Download Section 73 Double Angle Half Angle And Sum Product Identities 59d8ddd0fc79f562c Html




How Many Can You Derive From First Principles Ppt Download
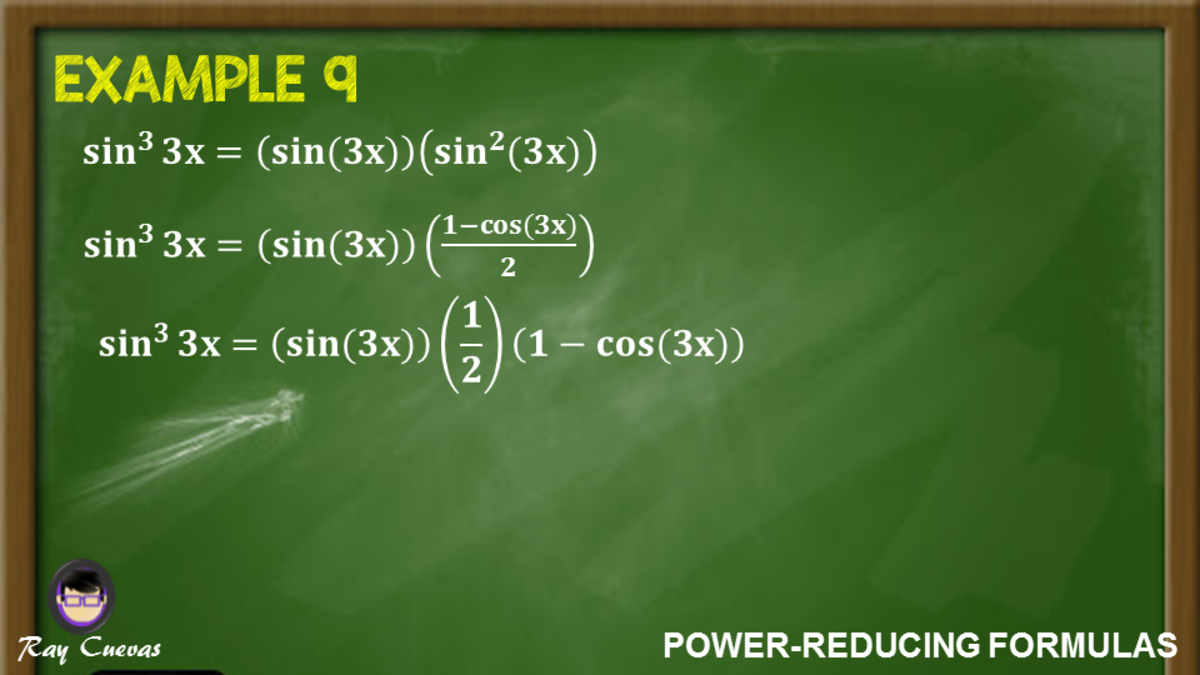



Power Reducing Formulas And How To Use Them With Examples Owlcation




How Do You Prove That Tanx Secx 1 Tanx Secx 1 1 Sinx Cosx Socratic




If Tan 2 X Sec X A 0 Has Atleast One Solution Then Complete Set Of V Askiitians




Tan2x Sec2x ただの悪魔の画像
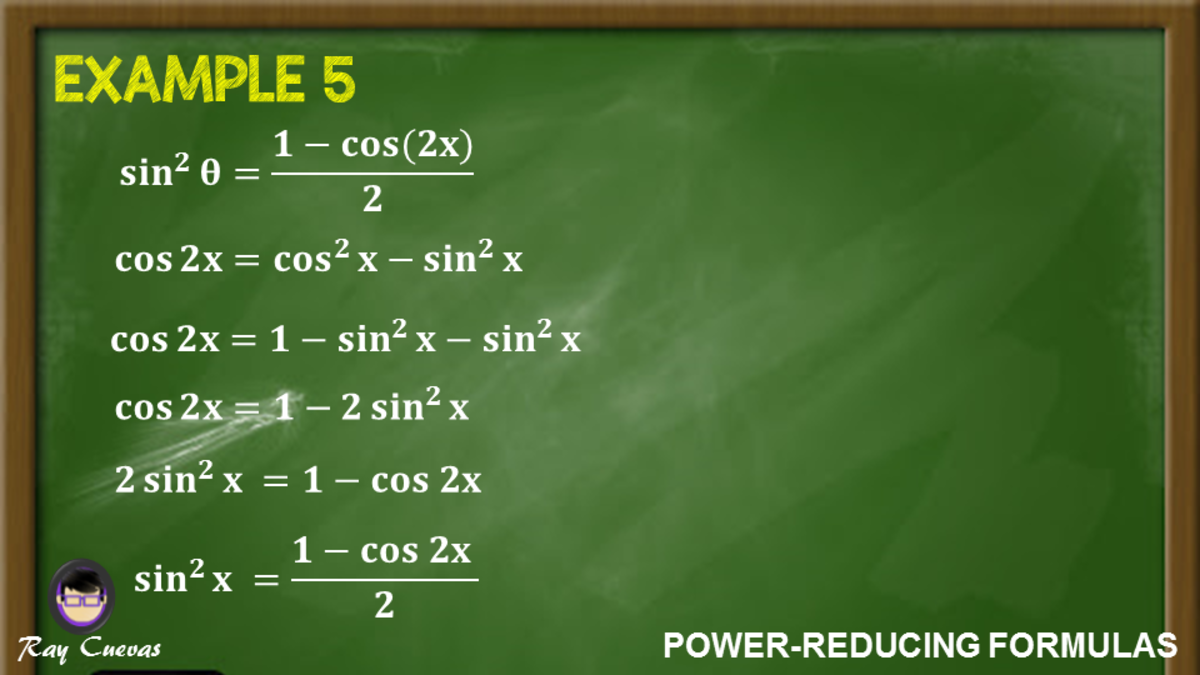



Power Reducing Formulas And How To Use Them With Examples Owlcation



3




Prove That There Are No Real Values Of X For Which Gauthmath




Cos Sin Tan Csc Sec Cot




Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf



2




Example 27 Find Value Of Tan Pi 8 Chapter 3 Class 11



2
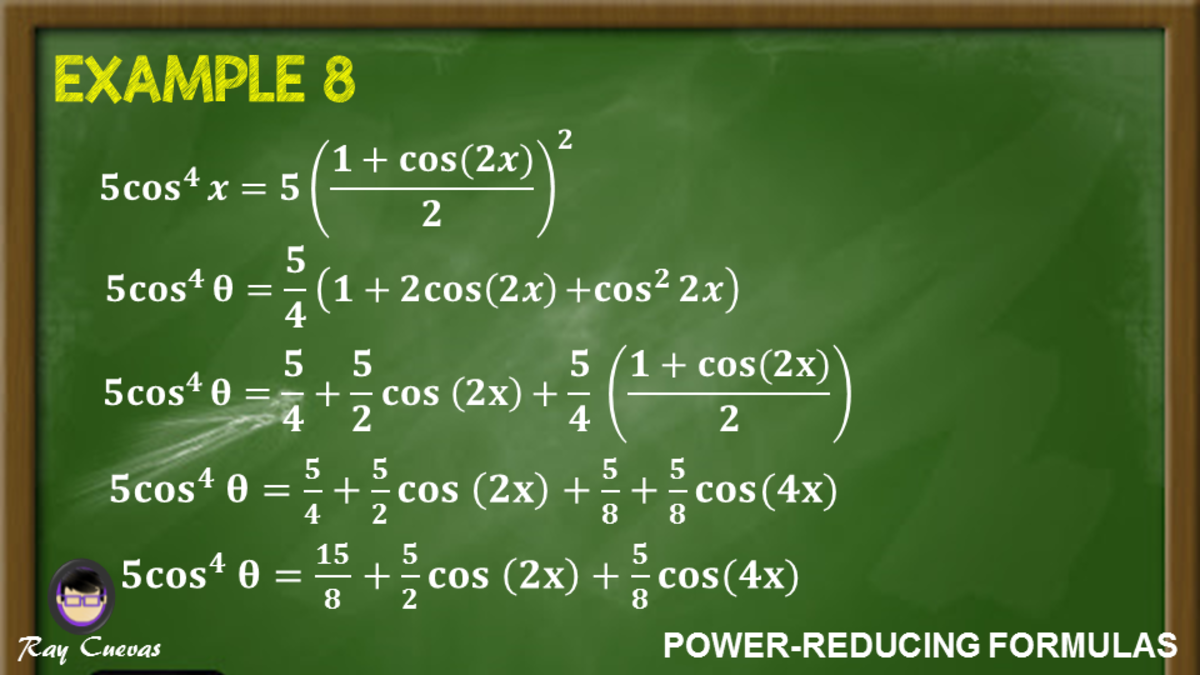



Power Reducing Formulas And How To Use Them With Examples Owlcation



1




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic
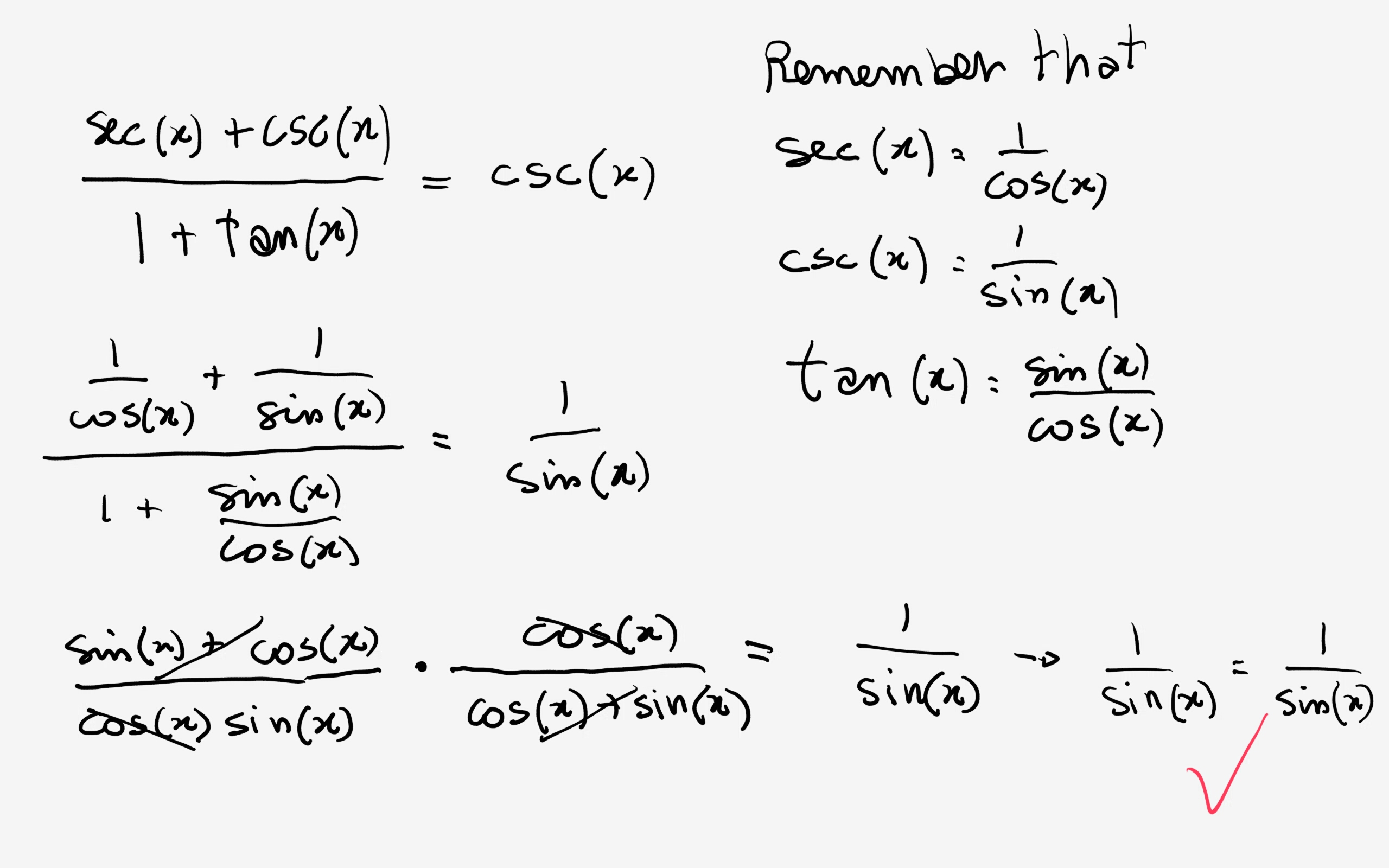



How Do You Prove Sec X Csc X 1 Tan X Csc X Socratic




If Cosx 1 10 Then Prove That Sec 2x Tan 2x 1 Trigonometric Value Sci Pi




Ppt Analytic Trig Powerpoint Presentation Free Download Id




Sec 2 X Cosec 2x Tan X Cot X Prove It Brainly In




Verify Identity Tan 2 X 1 Tan X Sec X 1 Sin X Cos 2 X Youtube




How Do You Verify 4tan 4 Tan 2x 3 Sec 2x 4tan 2x 3 Kinda Hard Please With All The Steps Thanks Socratic



0 件のコメント:
コメントを投稿